L'idea alla base di questi due metodi iterativi è quella di
``splittare'' la matrice 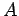 in
in 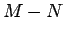 con
con
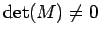 , quindi
, quindi
. Ovviamente non viene calcolata 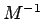 poiché
questa operazione è troppo costosa viene utilzzata la seguente formula:
1.1
poiché
questa operazione è troppo costosa viene utilzzata la seguente formula:
1.1
ed M deve essere di tipo
semplice. Affinché il metodo converga (
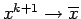 soluzione) è necessario che
soluzione) è necessario che
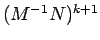 tenda a zero,
perché
tenda a zero,
perché
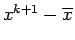 =
=
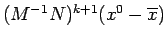 .
Da notare che a differenza delle fattorizzazioni, nei metodi iterativi
compare anche l'errore di troncamento, in quanto la convergenza
alla soluzione è di tipo asintotico e quindi è necessario
troncare la procedura ad un certo punto.
.
Da notare che a differenza delle fattorizzazioni, nei metodi iterativi
compare anche l'errore di troncamento, in quanto la convergenza
alla soluzione è di tipo asintotico e quindi è necessario
troncare la procedura ad un certo punto.
Subsections
2004-05-29
![]() in
in ![]() con
con
![]() , quindi
, quindi