Interpolazione mediante spline cubiche

Nel caso dell'interpolazione mediante polinomi abbiamo visto che sotto opportune condizioni per ogni funzione esiste una classe di polinomi interpolanti che la approssima con precisione sempre maggiore all'aumentare del grado del polinomio.

L'interpolazione mediante spline prevede un approccio diverso al problema dell'interpolazione. Le spline sono funzioni polinomiali a tratti che interpolano quindi la funzione tenendo fisso il grado del polinomio ma dividendo l'intervallo di interpolazione in $n$ intervalli più piccoli e considerando un polinomio diverso per ognuno di questi sottointervalli.

In particolare consideremo le spline cubiche cioè quelle di grado 3.

Formalmente, data una partizione $\Delta$ dell'intervallo di interpolazione $[a,b]$,

$$\Delta=\{a=x_{0}<x_{1}<\ldots<x_{n}=b\}$$

$s_{3}(x)$ è una spline di grado $3$ su $\Delta$ se:

1. $s_{3}(x) \vert _{[x_{i-1},x_{i}]} \in \prod_{3}$
2. $s_{3}(x) \in C^{(2)} ([a,b])$

$s_{3}(x)$ si dice interpolante $f(x)$ se: $s_{3}(x_{i})=f_{i} \quad \textrm{i=0,1,\ldots,n}$.

Inoltre si può dimostrare che $S_{3,\Delta} =\{ s_{3}(x): s_{3}(x)$ è una spline cubica su $\Delta \}$ è uno spazio vettoriale di dimensione $n+3$. La dimensione dello spazio $S_{3,\Delta}$ implica che servono $n+3$ condizioni per determinare univocamente una spline cubica; di queste $n+1$ derivano dalle condizioni di interpolazione.

Abbiamo implementato il metodo delle spline cubiche naturali che prevede di scegliere queste due ulteriori condizioni.

$$s_3^{\prime\prime}(a)=s_3^{\prime\prime}(b)=0$$

Per un calcolo efficiente della spline cubica naturale interpolante una funzione consideriamo la partizione

$$\Delta=\{a=x_{0}<x_{1}<\ldots<x_{n}=b\}$$

e definiamo

$$h_i=x_i-x_{i-1} \quad i=2 \ldots n$$

La derivata di $s_{m}$ è una spline di grado $m-1$, quindi:

• $s_{3}^{\prime}(x) \quad \textrm{\\lq e una spline di grado 2 su} \quad \Delta$
• $s_{3}^{\prime\prime}(x) \quad \textrm{\\lq e una spline di grado 1 (lineare) su} \quad \Delta$

Se indichiamo con $I_{i}$ l'i-esimo intervallo

$$I_{i}=[x_{i-1},x_{i}]$$

e con

$$M_{i}=s_{3}''(x_{i}), \quad i=0,\ldots,n$$

ricavando l'equazione di $s_{3}''(x) \vert _{I_{i}}$ che è il segmento di retta che unisce i punti $(x_{i-1}; M_{i-1})$ e $(x_{i}; M_{i})$ e integrando due volte per trovare l'espressione di $s_{3}(x)$ si ottengono i seguenti risultati:

$$s_{3}'(x) \vert _{I_{i}}= \frac{(x-x_{i-1})^{2}M_{i} - (x_{i}-x)^{2}M_{i-1}} {2h_{i}} + C_{i}$$ (3.4)

$$s_{3}(x) \vert _{I_{i}}= \frac{(x-x_{i-1})^{3}M_{i}+(x_{i}-x)^{3}M_{i-1}} {6h_{i}} + C_{i}(x-x_{i-1}) + D_{i}$$ (3.5)

dove

$$C_i = \frac{f_{i}-f_{i-1}} {h_{i}} - \frac{h_i}{6}(M_i-M_{i-1})$$

$$D_i = f_{i-1}-\frac{h_{i}^{2}}{6}M_{i-1}$$

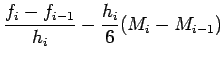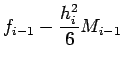Andiamo ora ad imporre la condizione di continuità della derivata prima. Infatti, come abbiamo detto, una spline cubica dev'essere, per definizione ,di classe $C^{(2)}$.

$$s_3^{\prime}(x_i)\vert _{I_i}=s_3^{\prime}(x_i)\vert _{I_{i+1}}$$ (3.6)

Otteniamo in questo modo $n-1$ condizioni che permettono di ricavare gli $M_i$ incogniti (dalla definizione di spline cubica naturale si ha $M_0=M_n=0$).

Facendo le opportune sostituzioni nella (3.6) si ottengono $n-1$ equazioni della forma

$$h_{i}M_{i-1}+2(h_i+h_{i+1})M_i+h_{i+1}M_{i+1}=6\delta_{i}$$

dove

$$\delta_i=\frac{f_{i+1}-f_{i}}{h_{i+1}}-\frac{f_i-f_{i-1}}{h_i}$$

Il sistema da risolvere è il seguente

$$\left( \begin{array}{ccccc} 2(h_{1}+h_{2}) & h_{2} & & & 0 \... ...ots \\ \\ \\ \\ \vdots \\ \delta_{n-1} \end{array}\right)$$

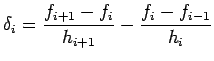
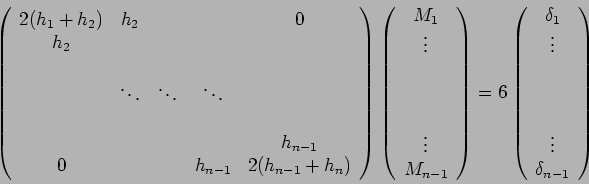
La matrice dei coefficienti di questo sistema è tridiagonale e simmetrica, a diagonale dominante, definita positiva e quindi non singolare, il problema è quindi ben posto.