Ascisse di Cebyshev
Abbiamo visto nel caso della funzione 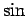 che un polinomio di grado
maggiore costituiva una approssimazione migliore della funzione. Ci
aspetteremo quindi che all'aumentare del grado del polinomio
interpolante questo approssimi sempre meglio la funzione, e che
all'aumentare di
che un polinomio di grado
maggiore costituiva una approssimazione migliore della funzione. Ci
aspetteremo quindi che all'aumentare del grado del polinomio
interpolante questo approssimi sempre meglio la funzione, e che
all'aumentare di 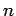 la famiglia di polinomi interpolanti tenda alla
funzione.
la famiglia di polinomi interpolanti tenda alla
funzione.
Questo non è vero se scegliamo le ascisse a distanza costante
nell'intervallo di approssimazione. Consideriamo ad esempio la
funzione di Runge così definita
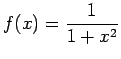 |
(3.1) |
nell'intervallo ![$ [-5, 5]$](img304.png) .
Vediamo i grafici dei polinomi interpolanti la
.
Vediamo i grafici dei polinomi interpolanti la 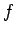 definita in
3.1 di grado crescente. Per
definita in
3.1 di grado crescente. Per 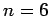 (cioè
(cioè
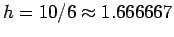 ) si ha il grafico in figura 3.3.
L'approssimazione è accettabile. Proviamo ad aumentare il grado: con
un polinomio di grado 9 (fig. 3.4) il risultato è
ancora abbastanza buono. Se il polinomio è di grado 12 diventa
evidete che l'approssimazione della funzione è pessima nel primo e
nell'ultimo intervallo della partizione (fig. 3.5).
Alzando il grado a 20 si ottiene il risultato disastroso della figura
3.6
) si ha il grafico in figura 3.3.
L'approssimazione è accettabile. Proviamo ad aumentare il grado: con
un polinomio di grado 9 (fig. 3.4) il risultato è
ancora abbastanza buono. Se il polinomio è di grado 12 diventa
evidete che l'approssimazione della funzione è pessima nel primo e
nell'ultimo intervallo della partizione (fig. 3.5).
Alzando il grado a 20 si ottiene il risultato disastroso della figura
3.6
Figura 3.3:
Interpolazione della funzione di Runge con un polinomio di
grado 6 nell'intervallo ![$ [-5; 5]$](img308.png) . Ascisse a distanza costante
. Ascisse a distanza costante
|
|
Figura 3.4:
Interpolazione della funzione di Runge con un polinomio di
grado 9 nell'intervallo ![$ [-5; 5]$](img308.png) . Ascisse a distanza costante
. Ascisse a distanza costante
|
|
Figura 3.5:
Interpolazione della funzione di Runge con un polinomio di
grado 12 nell'intervallo ![$ [-5; 5]$](img308.png) . Ascisse a distanza costante
. Ascisse a distanza costante
|
|
Figura 3.6:
Interpolazione della funzione di Runge con un polinomio di
grado 20 nell'intervallo ![$ [-5; 5]$](img308.png) . Ascisse a distanza costante
. Ascisse a distanza costante
|
|
La scelta delle ascisse di Cebyshev risolve questo problema. Le
ascisse di Cebyshev sono definite in ![$ [-1; 1]$](img312.png) da
da
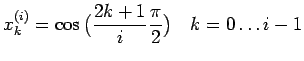 |
(3.2) |
Nela (3.2) 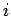 è il grado del polinomio interpolante.
è il grado del polinomio interpolante.
Per riportare le ascisse dall'intervallo ![$ [-1; 1]$](img312.png) a un generico
intervallo
a un generico
intervallo ![$ [a;b]$](img314.png) si usa questa formula, che trasforma
si usa questa formula, che trasforma
![$ x \in [-1;
1]$](img315.png) in
in
![$ X \in [a;b]$](img316.png) :
:
Con le ascisse di Cebyshev i risultati ottenuti con la funzione di
Runge sono infatti migliori e si può vedere che all'aumentare del
grado del polinomio interpolante il polinomio tende effettivamente
alla funzione. Nelle figure 3.7-3.10
si vedono i grafici dei polinomi interpolanti la funzione di Runge di
grado 6,9,12,20 scegliendo le ascisse di interpolazione di Cebyshev
Figura 3.7:
Interpolazione della funzione di Runge con un polinomio di
grado 6 nell'intervallo ![$ [-5; 5]$](img308.png) . Ascisse di Cebyshev
. Ascisse di Cebyshev
|
|
Figura 3.8:
Interpolazione della funzione di Runge con un polinomio di
grado 9 nell'intervallo ![$ [-5; 5]$](img308.png) . Ascisse di Cebyshev
. Ascisse di Cebyshev
|
|
Figura 3.9:
Interpolazione della funzione di Runge con un polinomio di
grado 12 nell'intervallo ![$ [-5; 5]$](img308.png) . Ascisse di Cebyshev
. Ascisse di Cebyshev
|
|
Figura 3.10:
Interpolazione della funzione di Runge con un polinomio di
grado 20 nell'intervallo ![$ [-5; 5]$](img308.png) . Ascisse di Cebyshev
. Ascisse di Cebyshev
|
|
2004-05-29
![\includegraphics[width=0.65\textwidth]{RungeAscCost6.eps}](img307.png)
![\includegraphics[width=0.65\textwidth]{RungeAscCost9.eps}](img309.png)
![\includegraphics[width=0.65\textwidth]{RungeAscCost12.eps}](img310.png)
![\includegraphics[width=0.65\textwidth]{RungeAscCost20.eps}](img311.png)
![]() da
da
![]() a un generico
intervallo
a un generico
intervallo ![]() si usa questa formula, che trasforma
si usa questa formula, che trasforma
![]() in
in
![]() :
:
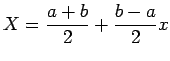
![\includegraphics[width=0.65\textwidth]{RungeAscCeby6.eps}](img318.png)
![\includegraphics[width=0.65\textwidth]{RungeAscCeby9.eps}](img319.png)
![\includegraphics[width=0.65\textwidth]{RungeAscCeby12.eps}](img320.png)
![\includegraphics[width=0.65\textwidth]{RungeAscCeby20.eps}](img321.png)