Per ottenere un algoritmo efficiente per il calcolo del polinomio
interpolante è necessario abbandonare la rappresentazione del
polinomio interpolate nella base canonica ed adottare una base diversa
per lo spazio 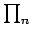 .
Una possibile base è la base di Newton, così definita
ricorsivamente:
In pratica si ha
.
Una possibile base è la base di Newton, così definita
ricorsivamente:
In pratica si ha
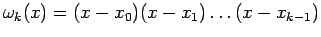 da cui
segue che
da cui
segue che
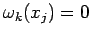 per
per 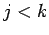 .
.
Si dimostra che
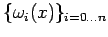 è una base per
è una base per
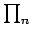 . Il polinomio interpolante di grado
. Il polinomio interpolante di grado 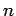 interpolante una funzione
può essere quindi espresso come
interpolante una funzione
può essere quindi espresso come
I coefficienti sono dati dalle differenze divise così
definite:
Subsections
2004-05-29
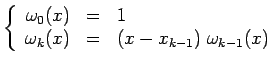
![]() è una base per
è una base per
![]() . Il polinomio interpolante di grado
. Il polinomio interpolante di grado ![]() interpolante una funzione
può essere quindi espresso come
interpolante una funzione
può essere quindi espresso come
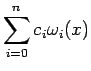
![$\displaystyle c_k =f[x_0,\ldots,x_k] =\sum_{i=0}^{k}{\frac{f_i}{\prod_{j=0,j \neq i}^{k}{(x_i-x_j)}}} \quad k=0 \ldots n$](img289.png)