Next: Fattorizzazione Up: Fattorizazione QR Previous: Vettore di Householder Indice
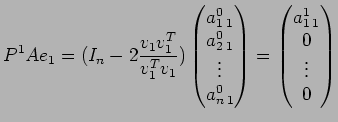
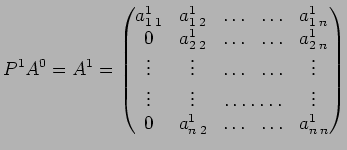
[x,A]=QRhouse(A,b) -
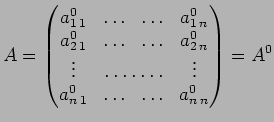
Data la matrice ![]() ed il vettore
ed il vettore
![]() la funzione fattorizza
la funzione fattorizza ![]() come il prodotto di due matrici
come il prodotto di due matrici ![]() con
con ![]() ortogonale ed
ortogonale ed ![]() triangolare superiore, secondo il metodo
di Householder e risolve il sistema
triangolare superiore, secondo il metodo
di Householder e risolve il sistema
![]() . La matrice
. La matrice ![]() viene memorizzata nella parte
triangolare superiore di
viene memorizzata nella parte
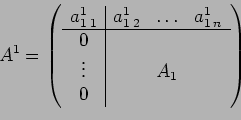
triangolare superiore di ![]() , ed al posto della
, ed al posto della ![]() vengono memorizzate nella
parte inferiore le parti significative dei vettori di
vengono memorizzate nella
parte inferiore le parti significative dei vettori di
![]() associati a ciascuna colonna della matrice originaria.
associati a ciascuna colonna della matrice originaria.
%QRHOUSE
%[x,A]=QRHOUSE(A,b)
%
%Pre: A è una matrice quadrata non singolare n x n;
% b vettore di lunghezza n
%
% La procedura fornisce la fattorizzazione QR di una matrice
% A e risolve
% il sistema lineare Ax=b; Q è una matrice
% ortogonale (Q'Q=I) e R è
% triangolare superiore.
% In x viene restituita la soluzione del sistema lineare mentre
% in A viene
%restituita una matrice che contiene nella sua
% parte triangolare superiore
% la matrice R e nella parte
% strettamente triangolare inferiore le componenti
% essenziali
% dei vettori di householder che generano la matrice Q
% See also HOUSE
function [x,A]=QRhouse(A,b)
n=length(b);
% beta = 2/(v' * v) con v vettore di houseolder
beta=zeros(1,n-1);
gamma=zeros(1,n);
for i=1:n-1
% adesso il vettore v si trova in
% A(i:n,i)
A(i:n,i)=house(A(i:n,i))';
beta(i)=2/([1;A(i+1:n,i)]'*[1;A(i+1:n,i)]);
% calcola v'*y con y vettore colonna corrente
for j=i+1:n
gamma(j)=([1;A(i+1:n,i)]'*A(i:n,j));
end
% aggiorna la riga i-esima
for t=i+1:n
A(i,t)=A(i,t)-gamma(t)*beta(i);
end
% viene aggiornata la sottomatrice in
% esame per colonne, moltiplicando per
% una matrice di Householder
for j=i+1:n
% prodotto vettoriale con fattore moltiplicativo
% aggiuntivo -gamma(k)*beta(i)
for k=i+1:n
A(k,j)=A(k,j)-gamma(j)*A(k,i)*beta(i);
end
end
end
% aggiornamento termine noto
x=b(:);
for i=1:n-1
temp=beta(i)*[1;A(i+1:n,i)]'*x(i:n);
x(i:n)=x(i:n)-temp*[1;A(i+1:n,i)];
end
x=solveU(A,x);
return
>> A A = 3.0000000000 1.0000000000 0.5000000000 0.8000000000 1.5000000000 9.0000000000 0.5000000000 0.6000000000 3.2000000000 4.0000000000 12.7000000000 3.2000000000 0.7000000000 3.2000000000 4.1000000000 11.3000000000 >> b b = 0.50000000000000 1.20000000000000 3.00000000000000 6.20000000000000 >> inv(A)*b ans = -0.01092762955907 0.09772671951632 0.08447073456824 0.49102600234596 >> QRHouse(A,b) ans = -0.01092762955907 0.09772671951632 0.08447073456824 0.491026002345962004-05-29