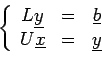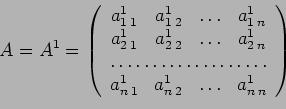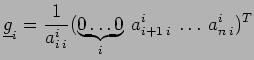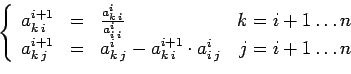La fattorizzazione LU consiste nello scomporre una matrice A nel prodotto
du due matrici, L triangolare inferiore ed U triangolare superiore
con la particolaritá che la matrice L ha sulla diagonale tutti 1;
se esiste tale fattorizzazione è unica.
Una volta fattorizzata A basta risolvere il seguente sistema
lineare per ottenere la soluzione
Se la matrice A è di ordine 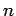 allora l'algoritmo consiste di
allora l'algoritmo consiste di 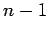 passi ognuno dei quali annulla gli elementi di una colonna
(quella corrispondente al numero del passo) sotto la diagonale principale
e lascia inalterato il ``lavoro svolto'' ai passi precedenti; tutto
questo si ottiene premoltiplicando a sinistra A per delle matrici
con struttura analoga alla L e chiamata matrici elementari di Gauss
.
Descrizione dell'algoritmo: con
passi ognuno dei quali annulla gli elementi di una colonna
(quella corrispondente al numero del passo) sotto la diagonale principale
e lascia inalterato il ``lavoro svolto'' ai passi precedenti; tutto
questo si ottiene premoltiplicando a sinistra A per delle matrici
con struttura analoga alla L e chiamata matrici elementari di Gauss
.
Descrizione dell'algoritmo: con 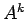 viene indicata la matrice
viene indicata la matrice
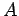 al passo k-esimo e con
al passo k-esimo e con
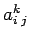 l'ememento in riga
l'ememento in riga 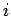 ,in colonna
,in colonna 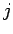 ed al passo
ed al passo 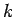 della matrice
della matrice 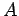 .
L'algoritmo parte con
e ricava
.
L'algoritmo parte con
e ricava 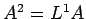 dove adesso
dove adesso 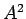 è
si nota che adesso nelle righe inferiori alla prima compare l'indice 2 in alto
e questo significa che l'algoritmo non modifica quello che era stato fatto
ai passi precedenti e che via via si vanno a modificare le righe inferiori
della matrice, lasciando inalterate le altre. Al passo i-esimo si ricava
è
si nota che adesso nelle righe inferiori alla prima compare l'indice 2 in alto
e questo significa che l'algoritmo non modifica quello che era stato fatto
ai passi precedenti e che via via si vanno a modificare le righe inferiori
della matrice, lasciando inalterate le altre. Al passo i-esimo si ricava
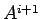 come i prodotto
come i prodotto 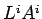 dove
dove
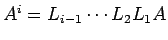 .
Di queste matrici
.
Di queste matrici 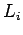 ce ne sono
esattamente
ce ne sono
esattamente 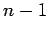 e la loro forma è del tipo
dove
e la loro forma è del tipo
dove
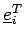 indica nel modo usuale l'i-esimo vettore
della base canonica di
indica nel modo usuale l'i-esimo vettore
della base canonica di 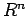 trasposto e
trasposto e
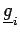 indica
l'i-esimo vettore di Gauss definito come
Se indichiamo con
indica
l'i-esimo vettore di Gauss definito come
Se indichiamo con 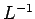 il prodotto
il prodotto
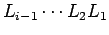 si ha
proporio che
si ha
proporio che 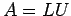 , infatti si ha che l'inversa di
, infatti si ha che l'inversa di 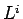 è
è
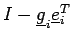 ed è triangolare inferiore
con tutti 1 sulla diagonale, e quindi lo è anche il loro prodotto.
L' algoritmo al passo i-esimo modifica la matrice nel seguente modo
e poichè vengono annullati
ed è triangolare inferiore
con tutti 1 sulla diagonale, e quindi lo è anche il loro prodotto.
L' algoritmo al passo i-esimo modifica la matrice nel seguente modo
e poichè vengono annullati 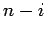 elementi sotto la diagonale, le
loro posizioni possono essege occupare dalle componenti significative
del vettore
elementi sotto la diagonale, le
loro posizioni possono essege occupare dalle componenti significative
del vettore
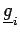 .
.
Subsections
2004-05-29